|
Home
NataData
Gucken
Lesen
Denken
Surfen
Orientieren
Impressum
| |
|

Rätseln, Wundern, Staunen
und Denken...
... von Zeit
zu Zeit gibt es hier neuen (nicht immer ernst gemeinten) Stoff.
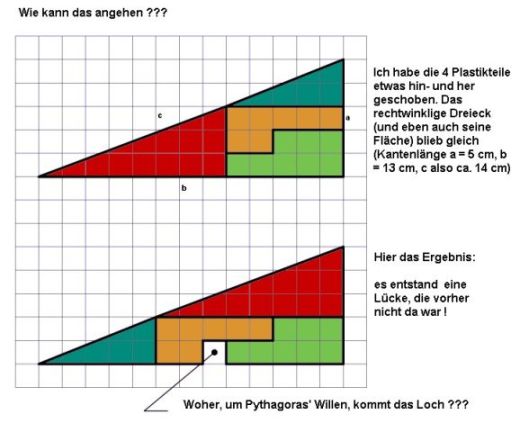
Woher
kommt
das Loch
(nicht ganz ernst gemeint) |
 |
|
Voynich-Manuskript |
Über
Simon Singhs Buch "Geheime
Botschaften" (eine exzellente und sehr spannende Einführung in die
Geschichte der
Kryptologie und
Kryptographie) bin ich das erste Mal auf eines der wohl rätselhaftesten
Schriftstücke der Geschichte gestoßen, das sogenannte
Voynich-Manuskript, benannt nach seinem "Finder"
Wilfried Michael Voynich, einem amerikanischer Büchersammler und
Antiquar polnischer Abstammung.

Das Manuskript wurde in einer
unbekannten Schrift und in einer unbekannten Sprache verfasst. Bis heute
ist es niemandem gelungen, auch nur ein Wort des Manuskriptes zu
entschlüsseln (was allerdings auch daran liegen könnte, dass es nichts
zu entschlüsseln gibt, wie immer mal wieder, z. B. jüngst von Andreas
Schinner behauptet wurde:
The Voynich Manuscript: Evidence of the Hoax Hypothesis).
Voynich entdeckte das Manuskript 1912
zusammen mit etwa 30 anderen wertvollen Manuskripten bei den
Jesuiten
der Villa Mondragone in
Frascati. Seit 1969 ist das Manuskript im Besitz der
Yale Universität, die auch hochauflösenden
Scans des Manuskripts bereitstellt.
Eine
exzellente Zusammenstellung der Geschichte, der Forschungen und
Theorien über dieses Manuskript findet sich in der englischen
Wikipedia.
Weitere Links:
(Retrieved from
http://en.wikipedia.org/wiki/Voynich_manuscript) |
|
Ziegenproblem |
 Dieses Problem
aus der
Stochastik hat mir schon viele hitzige Debatten mit Freunden
beschert. Das nette an ihm ist, dass es in einer Form daherkommt, die
jedem geläufig ist: Eine Quizshow. Dieses Problem
aus der
Stochastik hat mir schon viele hitzige Debatten mit Freunden
beschert. Das nette an ihm ist, dass es in einer Form daherkommt, die
jedem geläufig ist: Eine Quizshow.
Bei der Show kann der Kandidat ein
Auto gewinnen. Dem Spiel liegen die folgenden Regeln zugrunde:
1. Ein Auto und zwei
Ziegen werden zufällig auf drei Tore verteilt.
2. Zu Beginn des Spiels
sind alle Tore verschlossen, sodass Auto und Ziegen nicht sichtbar sind.
3. Der Kandidat wählt
ein Tor aus, welches aber vorerst verschlossen bleibt.
4. Hat der Kandidat das
Tor mit dem Auto gewählt, dann öffnet der Quizmaster zufällig ausgewählt
eines der beiden anderen Tore, hinter dem sich immer eine Ziege
befindet.
5. Hat der Kandidat ein
Tor mit einer Ziege gewählt, dann öffnet der Quizmaster dasjenige der
beiden anderen Tore, hinter dem die zweite Ziege steht.
6. Der Quizmaster
bietet dem Kandidaten an, seine Entscheidung zu überdenken und das
andere ungeöffnete Tor zu wählen.
7. Das vom Kandidaten
letztlich gewählte Tor wird geöffnet und er erhält das Auto, falls es
sich hinter diesem Tor befindet. Diese Regeln sind dem Kandidaten
bekannt.
Wie soll er sich (Punkt
6) entscheiden, um seine Gewinnchance zu maximieren?
Eine schöne Einführung findet sich in
der "ZEIT" unter dem Titel "Das
Rätsel der drei Türen" und (natürlich) in der Wikipedia auf
deutsch und
englisch. |
|
Gefangenendilemma
 |
Egoismus und
Rationalität, der Konflikt zwischen Kooperation und Defektion, Statistik
und Hoffnung, Realismus und Idealismus, Pessimismus und Optimismus,
Individuum und Kollektiv…
An wohl kaum einem anderen
Gedankenexperiment können diese Themen ähnlich zugespitzt überdacht
werden, als am (mittlerweile klassischen) sog. Gefangenendilemma (und
seinen Varianten):
"Zwei Gefangene
werden verdächtigt, gemeinsam eine Straftat begangen zu haben. Die
Höchststrafe für das Verbrechen beträgt fünf Jahre. Beiden Gefangenen
wird nun ein Handel angeboten, der beiden bekannt ist. Wenn einer
gesteht, und somit seinen Partner belastet, kommt er ohne Strafe davon -
der andere muss die vollen fünf Jahre absitzen. Entscheiden sich beide
zu schweigen, bleiben nur Indizienbeweise, die aber ausreichen, um beide
für zwei Jahre einzusperren. Gestehen aber beide die Tat, erwartet jeden
eine Gefängnisstrafe von vier Jahren. Nun werden die Gefangenen
unabhängig voneinander befragt. Es besteht weder vor noch während der
Befragung die Möglichkeit für die beiden, sich untereinander
abzusprechen."
Wie sollten sie entscheiden, und warum?
Ein Überblick findet sich wie immer in der Wikipedia:
Gefangenendilemma
... und an diversen
anderen Stellen. |
|
Currys Paradoxon
 |
"Wenn dieser
Satz wahr ist, dann wurde das Curry in Berlin erfunden."
Ups! 'Got the paradox?
Falls nicht, empfehle ich den Eintrag in der
Stanford
Encyclopedia of Philosophy über
Curry's
Paradox.
Assoziationen zu
Russells Antinomie oder zum
Lügner Paradoxon sind begründet. |
|
Der "verschwundene" Euro
 |
Drei Männer
nehmen sich ein Hotelzimmer. Sie zahlen 30,- Euro an der Rezeption. Der
Manager bemerkt später, dass das Zimmer nur 25,- Euro kostet und gibt
dem Boy 5,- Euro, die er zurückbringen soll. Auf dem Weg zum Hotelzimmer
bemerkt der Boy, dass man 5,- Euro nicht gerecht an drei Leute verteilen
kann, behält deshalb 2,- Euro für sich und gibt jedem Gast 1,- Euro
zurück. Damit hat also jeder der Männer 10,- Euro bezahlt und 1,- Euro
zurückbekommen, was bedeutet, dass jeder 9,- Euro bezahlt hat, alle
zusammen also 27,- Euro. Der Boy hat 2,- Euro abgezweigt, was in der
Summe 29,- Euro ergibt. Wo ist der fehlende Euro?
(Das erinnert mich an die
beliebten Anrufe im Help-Center: "Tach, ich hätt' da gern mal ein
Problem...") |
|
P = NP |
Wem das alles
bisher zu kindisch ist, kann ja versuchen, eine Million Dollar zu
verdienen, die das Clay
Mathematics Institute of Cambridge, Massachusetts (CMI) zur
Jahrtausendwende jeweils für die Lösung eines der sieben größten
Millennium-Probleme der Mathematik
ausgelobt hat. Lediglich eines wurde inzwischen offenbar gelöst
(indem der Beweis für die
Poincaré-Vermutung erbracht wurde, siehe auch den
Zeit-Artikel),
womit es noch sechs Millionen Dollar zu verdienen gäbe.
Allein das Unterfangen, eines der Probleme
verstehen zu wollen, dürfte genug zu denken geben… |
|
Paradoxien |
Hier gibt es Links zu den
bekanntesten
Paradoxien aus vielen verschiedenen Bereichen. |
|
Links |
Auf der "Surfen"-Seite
gibt es weiteren Stoff. |
|
to be continued

Diese Seite ist erdstrahlenfrei
nach ER-SUP/2582954
|
![]()